Häufigkeitsanalyse



Um einen durch Caesar-Verschiebung verschlüsselten Text zu knacken, war es viel zu mühsam und zeitaufwändig, alle Schlüssel auszuprobieren.

Wie also konnte man eine verschlüsselte Botschaft schneller knacken?

Im 9. Jahrhundert ist dem arabischen Gelehrten al-Kindi (Orient) zum ersten Mal die unterschiedliche Häufigkeitvon Buchstaben in einer natürlichen Sprache bewusst geworden; was eine Möglichkeit der Entschlüsselung darbot. Natürliche Sprachen haben relativ wenige Buchstaben, die sehr unterschiedliche Häufigkeiten aufweisen.

Hier einige Beispiele:

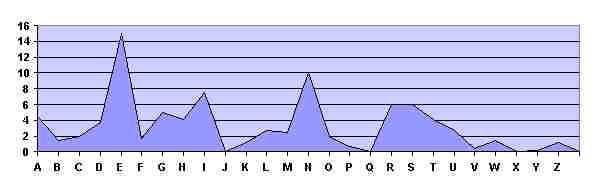
1. deutsche Sprache:




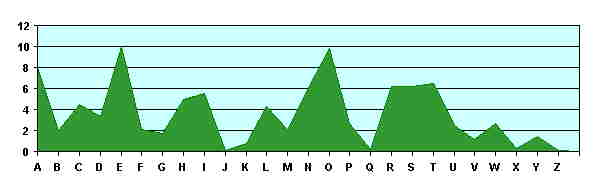
2. englische Sprache:




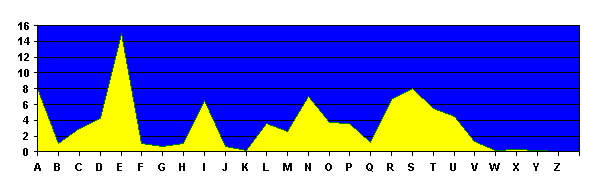
3. französische Sprache:




Um diese Buchstabenverteilung herauszufinden, haben wir das Programm verwendet.
Sie können es gerne selber einmal ausprobieren. Klicken Sie dazu bitte auf das unterstrichene Wort.

Wir wollen das weitere Vorgehen der Sprachwissenschaftler und Statistiker an der deutschen Sprache veranschaulichen.

Anhand Abb1.1 erkennt man sofort eine charakteristische Verteilung der Buchstaben in der deutschen Sprache:

• Die e-Spitze und der n-Gipfel
• Der b-c-d-Anstieg mit anschließender e-Spitze

Diese Struktur findet man auch in jedem monoalphabetisch verschlüsselten deutschen Text (mittels Caesarverschiebung).


Die 5 häufigsten Buchstaben e-n-i-s-r decken bereits 50 % der vorkommenden Buchstaben ab, die häufigsten 10 dann über 75 %.

Zuerst ermittelt der Kryptoanalytiker nun die Häufigkeitsverteilung der Buchstaben im abgefangenen Geheimtext, den er eventuell als Stabdiagramm darstellt. So erkennt er wenigstens die beiden häufigsten Buchstaben, denn bei der Caesar-Verschlüsselung wird sich eine ähnliche Verteilunsfunktion ergeben, nur verschoben.
Im zweiten Schritt schaut er sich die Buchstaben paarweise an.
Das Bigramm der deutschen Sprache zeigt die häufigsten Kombinationen.

Bigramm	Buchstabenpaar	Rel.Häufigkeit
1	en	0.0388
2	er	0.0375
3	ch	0.0275
4	te	0.026
5	de	0.02
6	nd	0.0199
7	ei	0.0188
8	ie	0.0179
9	in	0.0167
10	es	0.0152

Damit man einen Text überhaupt entschlüsseln kann, muss er eine gewisse
Länge haben, da es sonst schwierig ist, die Häufigkeitsanalyse durchzuführen.


Wir möchten dieses Vorgehen der Kryptoanalytiker nun an einem Beispiel verdeutlichen.
Hierzu verwenden wir einen Teil des monoalphabetisch verschlüsselten Text der
Caesar-Verschlüsselung , der über diesen hinaus geht.

"JXQCHLQIDFK: PDQVLHKWQXUPLWGHPKHUCHQJXW.
GDVZHVHQWOLFKHLVWIXHUGLHDXJHQXQVLFKWEU.
'GDVZHVHQWOFKHLVWIXHUGLHDXJHKXQVLFFKWEU',
ZLHGHUKROWHGHUNOHLQHSULQC,XJHVVLFKCXPHUNHQ.
'GLHCHFW;GLHGXIXHUGHXQHURVHYHUORUHQKDVW,
VLHPDFKWGHLQHURVHVRZLFKWLJ.'
'GLHCHLW;GLHLFKIXHUPHLQHURVHYHUORUHQKDEH ...',
VDJWHGHUNOHLQHSULQC,XJHVVLFKCXPHUNHQ.
'GlEPHQFKHQKDEQGLHVHZDKUKHLWYHUJHVVHQ',
VDJWHGHUIXFKS."

1. Bestimmung der relativen Häufigkeit der Buchstaben mittels des Programms
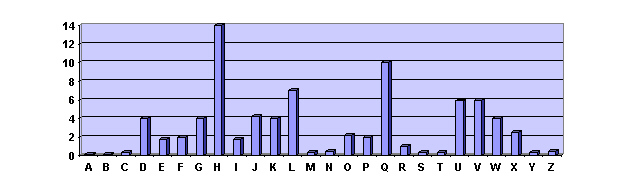
2. Aufstellen eines Stabdiagramms

3. Aufstellen eines Bigramms

Da der Buchstabe 'h' am häufigsten im Geheimtext vorkommt, kann es eigentlich nur das 'e' sein.
Der zweithäufigste Buchstabe ist das 'q'. Er kommt in der Kombination 'qh' als häufigstes Bigramm vor. Folglich ist 'q' eindeutig das 'n'.
Es gibt nur zwei Bigramme der deutschen Sprache mit ebendieser Häufigkeit, in denen der zweite Buchstabe ein n ist: en und in.
Damit ist auch das 'i' ent schlüsselt, es war ein 'l'.
Das zweithäufigste Bigramm der deutschen Sprache ist 'er'. Das 'e' haben wir identifiziert, es heißt jetzt 'h'.
Das Paar 'hu' - das einzige, das mit 'h' beginnt und noch nicht identifiziert ist - kommt in Frage, einmal das gesuchte 'er' gesesen zu sein.
Das 'u' kommt mit einer relativen Häufigkeit von 5,9 % im Geheimtext vor, das 'r' hat in der deutschen Sprache die Häufigkeit 6 %, das scheint zu passen.
Wenn wir die Buchstaben aus der Rückersetzung einsetzen (mittels eines Programms), so entsteht ein Lückentext, der aufgefüllt werden muss.
Man kann einzelne Wörter erkennen, z.B. PHLQH. _eine kann nur 'deine', 'meine' oder 'seine' heißen.
Durch Probieren findet man relativ schnell die Lösung des verschlüsselten Textes.
Das einzigen Problem dabei ist, dass die Worte einfach hintereinander geschrieben sind, was die Bigrammanalyse verzerrt.

Zusammenfassend kann man sagen, dass die Kryptoanalytiker die unterschiedlichen Häufigkeiten der Buchstaben in natürlichen Sprachen ausgenutzt haben, um momoalpabetisch verschlüsselte Texte zu knacken.
Man hat mittlerweile viele neue Verfahren gefunden, um Texte zu verschlüsseln.
Einige davon finden Sie auf den Seiten zur Kryptologie.